1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
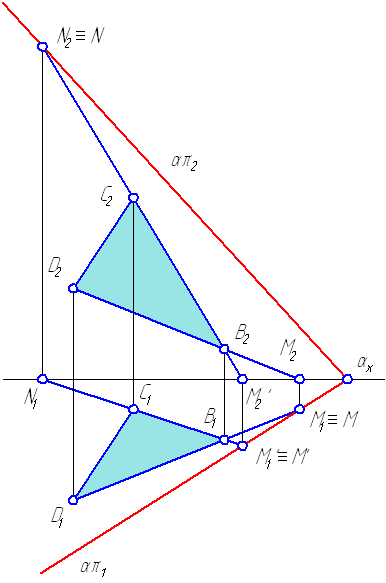
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
- (D2B2 ∩ OX) = M2;
- (MM1 ∩ D1B1) = M1 = M;
- (C2B2 ∩ OX) = M′2;
- (M′2M′1 ∩ C1B1) = M′1 = M′;
- (CВ ∩ π2) = N2= N;
- (MM′) ≡ απ1;
- (αxN) ≡ απ2.
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
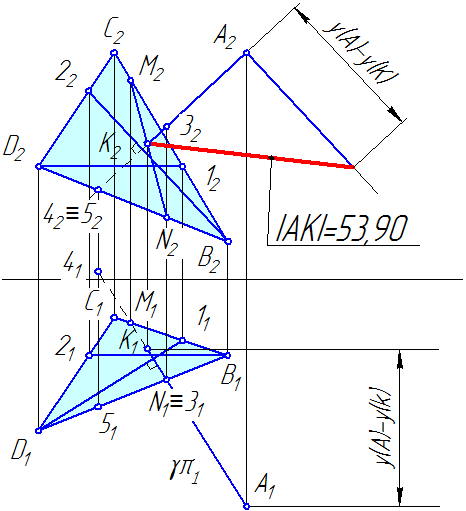
Рисунок 1.2 — Построение перпендикуляра к плоскости
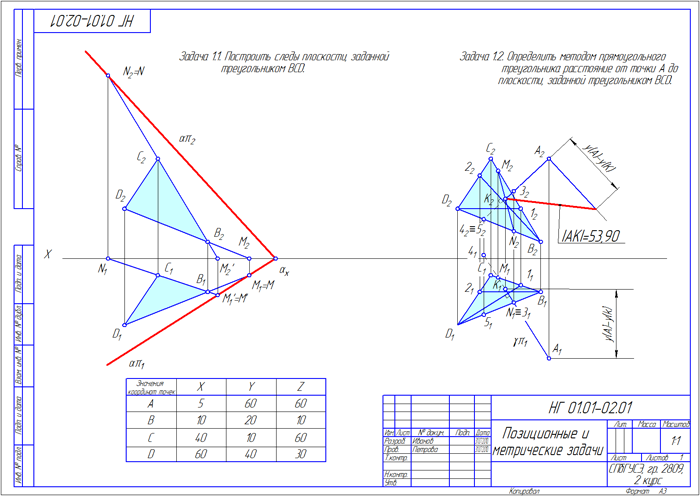
Рисунок 1.3 — Пример оформления контрольного задания №1
Видеопример выполнения задания №1
1.3. Варианты задания 1
| Вариант | Координаты (x, y, z) точек | |||
|---|---|---|---|---|
| А | В | С | D | |
| 1 | 15; 55; 50 | 10; 35; 5 | 20; 10; 30 | 70; 50; 40 |
| 2 | 80; 65; 50 | 50; 10; 55 | 10; 50; 25 | 75; 25; 0 |
| 3 | 95; 45; 60 | 130; 40; 50 | 40; 5; 25 | 80; 30; 5 |
| 4 | 115; 10; 0 | 130; 40; 40 | 40; 5; 25 | 80; 30; 5 |
| 5 | 55; 5; 60 | 85; 45; 60 | 100; 5; 30 | 50; 25; 10 |
| 6 | 55; 5; 60 | 70; 40; 20 | 30; 30; 35 | 30; 10; 10 |
| 7 | 60; 10; 45 | 80; 45; 5 | 35; 0; 15 | 10; 0; 45 |
| 8 | 5; 0; 0 | 35; 0; 25 | 20; 0; 55 | 40; 40; 0 |
| 9 | 50; 5; 45 | 65; 30; 10 | 30; 25; 55 | 20; 0; 20 |
| 10 | 60; 50; 35 | 40; 30; 0 | 30; 15; 30 | 80; 5; 20 |
| 11 | 65; 35; 15 | 50; 0; 30 | 20; 25; 25 | 5; 0; 10 |
| 12 | 75; 65; 50 | 45; 10; 35 | 60; 20; 10 | 10; 65; 0 |
| 13 | 95; 0; 15 | 85; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 14 | 45; 40; 40 | 80; 50; 10 | 10; 10; 10 | 55; 10; 45 |
| 15 | 80; 20; 30 | 55; 30; 60 | 15; 10; 20 | 70; 65; 30 |
| 16 | 75; 35; 35 | 55; 30; 60 | 25; 10; 20 | 70; 65; 30 |
| 17 | 75; 65; 50 | 45; 5; 55 | 5; 45; 10 | 70; 20; 0 |
| 18 | 65; 15; 20 | 40; 5; 60 | 0; 5; 25 | 60; 60; 20 |
| 19 | 70; 20; 10 | 45; 15; 60 | 5; 10; 20 | 60; 65; 10 |
| 20 | 20; 50; 45 | 10; 20; 10 | 55; 50; 10 | 80; 0; 60 |
| 21 | 0; 5; 50 | 50; 50; 40 | 5; 55; 10 | 45; 5; 0 |
| 22 | 55; 50; 65 | 45; 55; 5 | 0; 10; 45 | 70; 0; 40 |
| 23 | 65; 5; 15 | 40; 60; 10 | 0; 20; 5 | 60; 20; 60 |
| 24 | 50; 20; 45 | 45; 60; 30 | 5; 20; 10 | 60; 30; 5 |
| 25 | 55; 15; 40 | 40; 50; 25 | 5; 15; 10 | 50; 40; 10 |
| 26 | 15; 45; 40 | 10; 25; 5 | 20; 10; 30 | 65; 40; 35 |
| 27 | 70; 30; 30 | 55; 30; 60 | 20; 5; 15 | 65; 60; 25 |
| 28 | 90; 0; 15 | 80; 45; 10 | 10; 10; 10 | 50; 10; 45 |
| 29 | 110; 10; 0 | 120; 35; 30 | 35; 5; 20 | 70; 20; 5 |
| 30 | 45; 40; 40 | 80; 45; 10 | 10; 10; 10 | 55; 10; 40 |




