Задание 4. Взаимное пересечение поверхностей

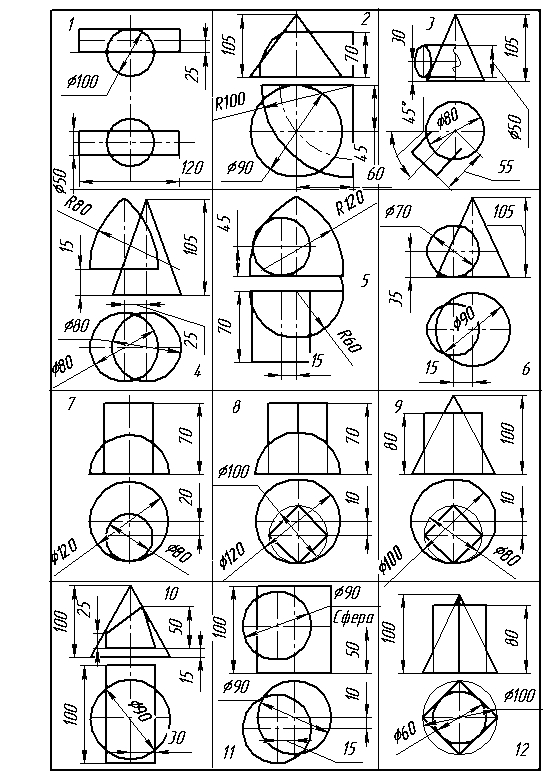
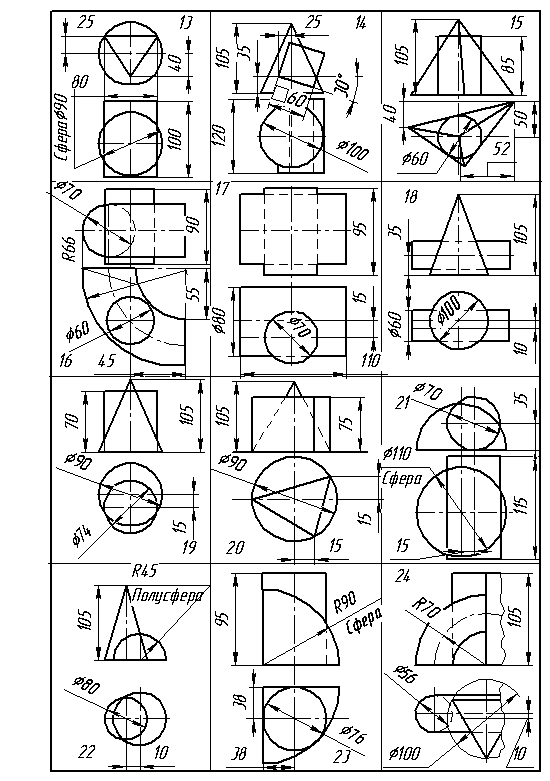
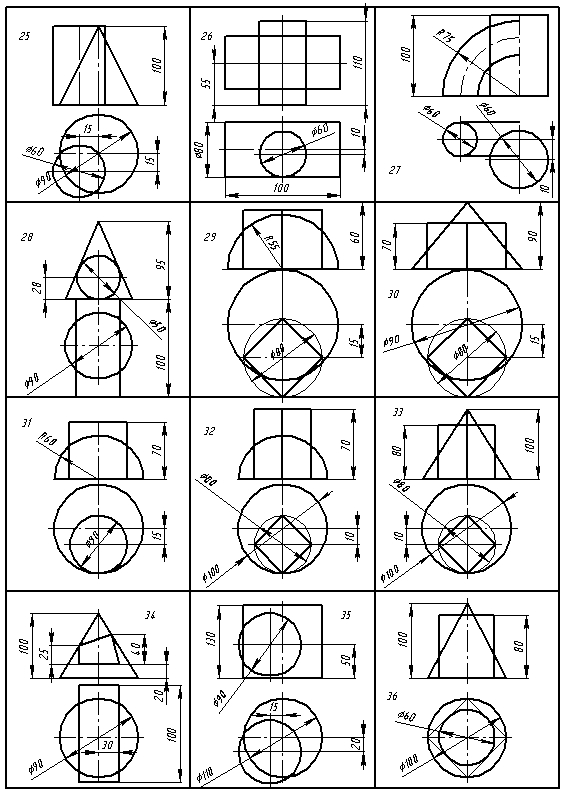
5.1. Условие задания

Построить линию пересечения поверхностей методом секущих плоскостей в соответствии с вариантом, предложенным преподавателем.

5.2. Рекомендации по выполнению задания

На ватмане формата А 4 или А 3, в зависимости от условия задачи, построить две проекции пересекающихся тел.Построение линии пересечения поверхностей рекомендуется выполнять в следующем порядке:

1. Определить, какие поверхности участвуют в пересечении;
2. Определить положение поверхностей относительно плоскостей проекций, при этом выяснить наличие поверхностей, перпендикулярных к плоскостям проекций;
3. Построить проекции характерных (опорных) точек, к которым относятся:

• очки, расположенные на границах видимости и линии пересечения;
• точки, расположенные на очерковых линиях, не являющихся границей видимости;
• экстремальные точки (высшая и низшая).

4. Соединить одноименные проекции точек линии пересечения.

Для построения линии пересечения поверхностей методом секущих плоскостей необходимо:

1. Провести вспомогательную секущую плоскость, выбрав её так, чтобы она пересекала обе заданные поверхности по простейшим линиям – окружностям или прямым;
2. Построить линии пересечения вспомогательной плоскости с обеими поверхностями;
3. Найти точки пересечения полученных линий;
4. С помощью ещё нескольких секущих плоскостей найти необходимое количество точек и их соединить.

ПРИМЕЧАНИЕ: построение следует начинать с отыскания характерных точек, а затем – промежуточных.

5.3. Пример выполнения задания

Рассмотрим задачу на построение линии пересечения поверхностей прямого кругового цилиндра и закрытого тора (рисунок 5.1).

Для построения линии пересечения потребуется профильная проекция заданных поверхностей, а в качестве вспомогательных секущих плоскостей следует воспользоваться горизонтальными плоскостями уровня γ_ν. Пересечение профильных очерков определяет опорные точки А и G (A₃, G₃). Фронтальные проекции этих точек  A₂и G₂ находим по горизонтальным линиям связи, а A₁ и G₁ – по координате y, измеренной от вертикальной плоскости симметрии цилиндра или от оси i (i₃ , i₁) тора.

Плоскость γ_ν рассекает тор по параллели и проходит через образующую фронтального очерка цилиндра. Пересечение их горизонтальных проекций определяет точки В (В₁ → В₂) и В′ (В’₁ → В′₂). Это самые высокие точки, и они же являются верхней границей видимости для цилиндра.

Аналогично находим  самые нижние точки F(F₁ → F₂) и F′ (F‘₁ → F′₂). ( для них посредник не обозначен, а точки F₁ и F‘₁ определены засечками из без построения всей параллели).

Точки С (С₃→  С₂ → С₁),  С’ (С’₃→  С’₂ → С’₁) и  Е (Е₃→  Е₂ → Е₁),  Е’ (Е’₃→  Е’₂ → Е’₁) пересечения главного меридиана тора с цилиндром определяются по линиям связи и не требуют дополнительных построений.

Точки D (D₁ → D₂) и D′ (D‘₁ → D′₂), принадлежащие образующей горизонтального очерка цилиндра, определяются с помощью посредника γ(γ³₃). На профильной проекции от i₃ измерим радиус параллели в плоскости γ³₃, этим радиусом строим окружность с центром i₁, и ее пересечение с очерком цилиндра определяет точки D₁и D‘₁.

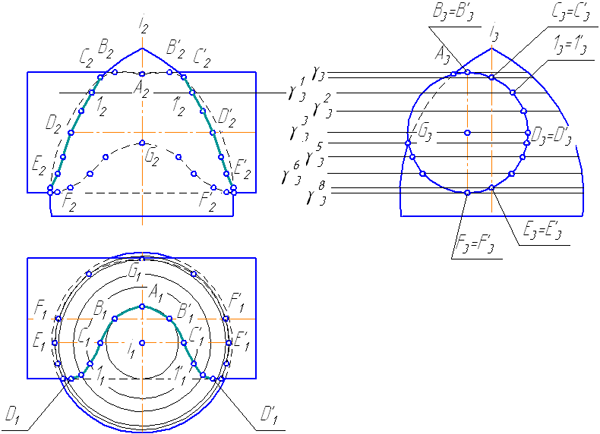
Рисунок 5.1 – построение линии пересечения поверхностей

Для определения случайных точек 1, 1^′ воспользуемся посредником γ¹ (γ¹₃), который пересекает цилиндр по образующей, находящейся на расстоянии y от вертикальной плоскости симметрии цилиндра.

Если на горизонтальной проекции расстояние  y отложить от оси цилиндра в соответствующую сторону, то мы построим горизонтальную проекцию этой образующей, а ее пересечение с проекцией соответствующей параллели тора определяет случайные точки 1₁и 1₁^′ линии пересечения. По линиям связи отмечаем точки 1₂ и 1₂^′ на фронтальной проекции.

Можно решить задачу и без профильной проекции заданных поверхностей, если построить дугу окружности основания радиусом R из проекции О₂ центра основания цилиндра, которую можно рассматривать как проекцию цилиндра на плоскость, перпендикулярную его оси. Тогда координата y для любой образующей плоскости γ определяется по этой дуге, как показано на Рисунке 5.1.

Полученные точки соединяются плавной кривой с учетом видимости.

Видеопример выполнения задания №4

5.4. Варианты заданий 4