6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды
Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.
Грани, пересекаясь, образуют ребра.
Ребра, пересекаясь, образуют вершины.
Рассмотрим два основных вида многогранников:
Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.
Упражнение
Дана пирамида, основание которой параллельно π1. Основание представляет собой некоторый треугольник.
S – вершина пирамиды (Рисунок 6.1).
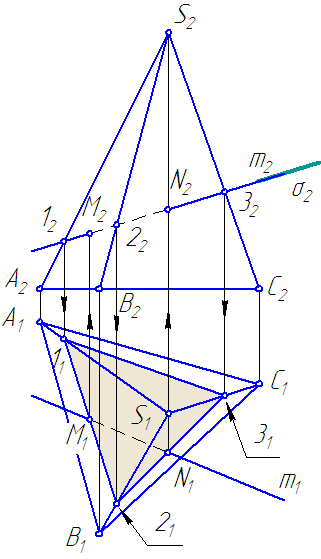
Рисунок 6.1 – Пересечение поверхности пирамиды прямой
Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.
Решение
- Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π2.
- Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.
Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).
Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.
- В сечении находим точки M и N принадлежащие прямой m.
- Определяем видимость прямой m.
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.
Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.
Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).
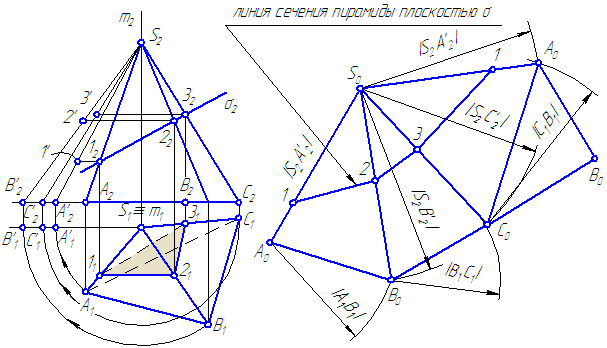
Рисунок 6.2 – Построение развёртки пирамиды
В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline{1},\overline{2},\overline{3}, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.
6.2. Призма. Развертка призмы
Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.
Упражнение
Дана призма, основания которой параллельны плоскости проекций π1.
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).
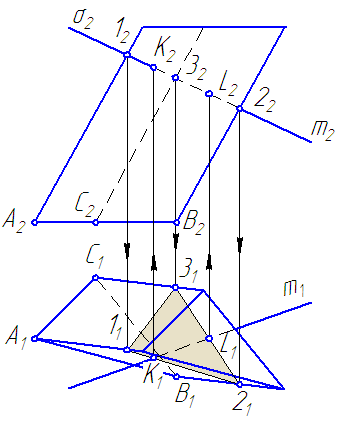
Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы
Порядок построения:
- Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π2.
- Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
- В сечении находим точки K и L принадлежащие прямой m.
- Определяем видимость прямой m. Если грань АВ на π2 видна, то точка К на π2 видима, грань ВС невидима, следовательно, точка Lневидима.
Рассмотрим наклонную призму. Пусть основание призмы параллельно π1, а ребра параллельны π2.
Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).
Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.
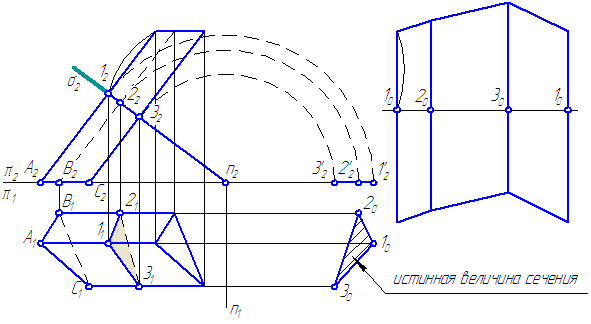
Рисунок 6.4 – Построение развёртки призмы
Порядок построения:
- Найдем истинную величину сечения – (102030), для чего повернём сечение (123) вокруг оси n⊥π2, (можно ввести ДПП π3//σ).
- Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
/10-20/; /20-30/; /30-10/.
- Проведём направления рёбер перпендикулярно этой линии через точки: 10; 20; 30 и отмерим вверх и вниз расстояния от нормального сечения (на π2) до верхнего и нижнего основания, откладывая их на линиях-ребрах.
6.3. Взаимное пересечение многогранников
В результате пересечения многогранников получим ломаную линию.
Возможны два случая пересечения многогранников (Рисунок 6.5):
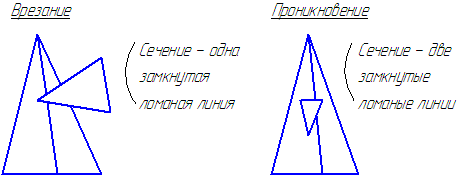
Рисунок 6.5 – Варианты пересечения многогранников
Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.
Звенья ломаной – линии пересечения граней.
Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.
Построенные точки соединить.
Упражнение
Построить линии пересечения призмы с пирамидой (Рисунок 6.6).
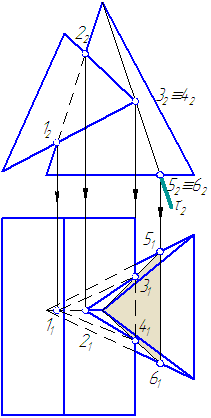
Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение
- Находим на π2 проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 12 и 22). Находим их горизонтальные проекции.
- Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 32 и 42), для чего используем вспомогательную плоскость τ⊥π2.
- Полученные на π1 точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 11-31, 11-21, 11-41 невидимы. Получили замкнутую линию пересечения пирамиды с призмой.
Упражнение
остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).
- По двум проекциям построить третью;
- На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
- Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
- Построить развёртку пирамиды с нанесением линии пересечения.
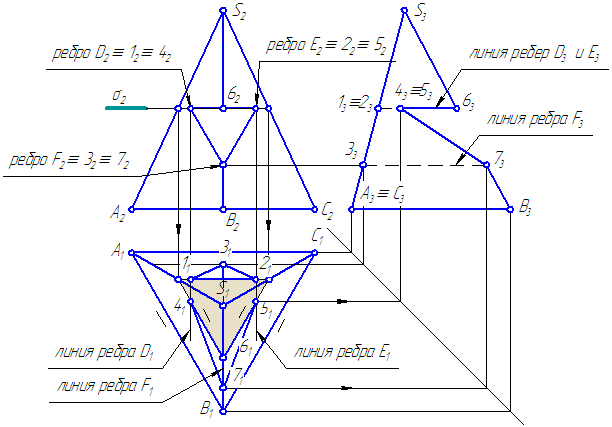
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение:
- Проводим линии рёбер призмы на всех проекциях.
- Введём плоскость σ⊥π2, σ//π1:
- σ//АВС – основанию пирамиды;
- σ пересекает пирамиду сечение подобно ΔА1В1С1.
Это сечение пересекается:
— с ребром D в двух точках 1 и 4;
— с ребром Е в двух точках 2 и 5.
Грань D2E2∩S2B2 =62.
Ребро F2∩S2B2 =72.
Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.
Построение развертки рассмотрено ранее.
6.4. Задачи для самостоятельной работы
1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).
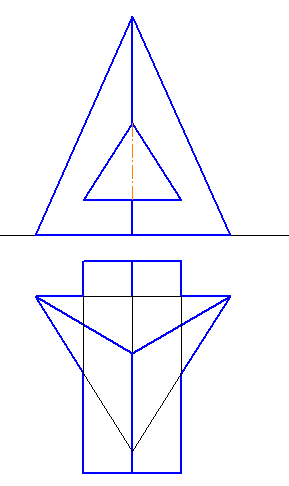
Рисунок 6.8
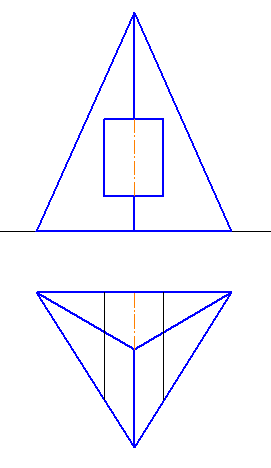
Рисунок 6.9
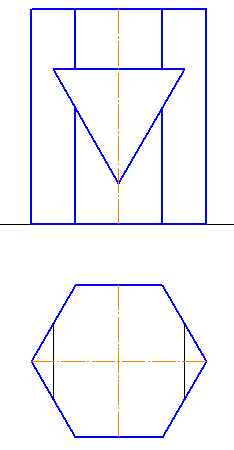
Рисунок 6.10
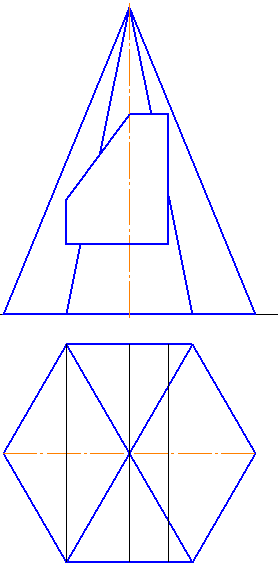
Рисунок 6.11




