В общем случае кривые поверхности второго порядка (цилиндр, конус, сфера) пересекаются по пространственной кривой четвертого порядка. Эта лекальная кривая строится по точкам.
В общем случае эти точки находятся как точки пересечения образующих одной поверхности с образующими другой, а потом точки последовательно соединяют линией с учётом видимости.
8.1. Частные случаи
Теорема Монжа 1. Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1).
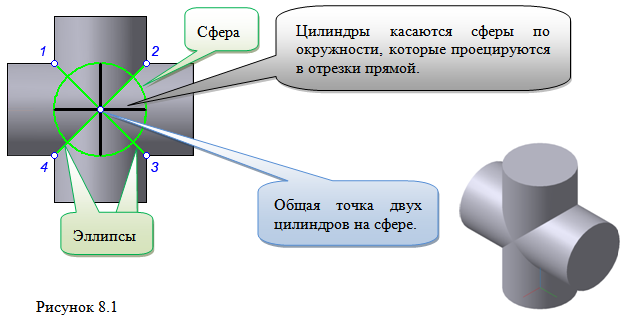
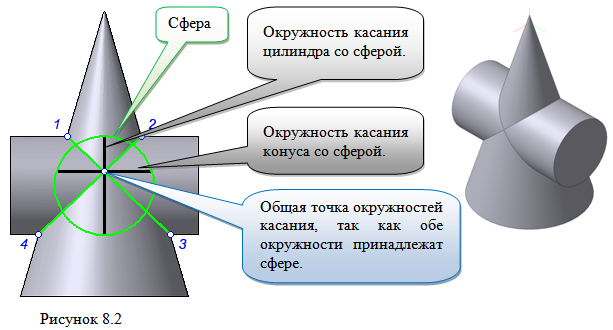
Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4.
Цилиндры пересекаются по эллипсам.
Крайние образующие пересекаются в точках 1, 2, 3, 4.
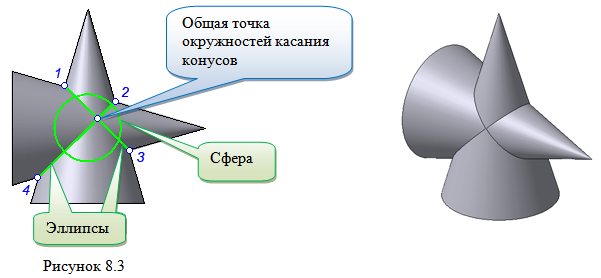
Теорема Монжа 2. Если две пересекающиеся поверхности второго порядка имеют общую плоскость симметрии, параллельную некоторой плоскости проекций, то на эту плоскость проекций линия их пересечения проецируется в кривую второго порядка. Если это условие не выполнено, то – в кривую четвертого порядка. Эту плоскость называют плоскостью параллелизма.
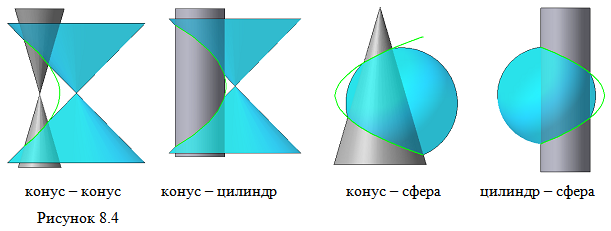
Рассмотрим четыре примера пересечения тел вращения, у которых оси вращения лежат в одной плоскости, параллельной плоскости проекций π2 (Рисунок 8.4). Следовательно, данная плоскость является плоскостью симметрии пересекающихся тел, параллельная плоскости проекций π2. Это означает, что линия пересечений тел проецируется на плоскость проекций π2 как кривая второго порядка – парабола.
8.2. Алгоритм построения точек кривой пересечения двух поверхностей
- Выполним анализ кривых пересечения цилиндра и конуса (Рисунок 8.5): у данных тел есть общая плоскость симметрии, параллельная плоскости проекций π2, следовательно, (согласно второй теореме Монжа) на π2 кривые пересечения тел 4-го порядка проецируются в виде кривых второго порядка. Поскольку при этом получается две ветви, следовательно, это будет гипербола.
- Строим характерные точки: пересечение крайних образующих на π2 цилиндра и конуса, точки 1, 2, 3, 4.
- Для нахождения точек, лежащих на крайних образующих на π1 цилиндра, введём плоскость σ⊥π2 и σ//π1 проходящую через фронтальную проекцию оси вращения цилиндра. В результате данная плоскость пересечет цилиндр по крайним образующим, а конус – по окружности радиусом Rσ. Построенные на π1 сечения пересекутся в точках 5, 6, 7, 8. По линии проекционной связи строим их фронтальные проекции.
- Для построения самых близких друг к другу точек кривой на π2 введём плоскость γ⊥π3, проходящую через вершину конуса и касательную к цилиндру. Данная плоскость пересечёт конус по треугольнику SAB. Построив образующие конуса SA, SB и цилиндра 11-12, на их пересечении определим точки 11, 12. Точки 9, 10 построим симметрично точкам 11 и 12.
- Для построения дополнительных промежуточных точек, можно ввести вспомогательные секущие плоскости (посредники) параллельно σ.
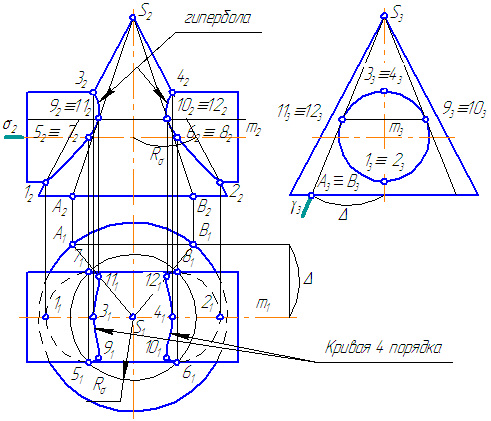
Рисунок 8.5 – Построение линии пересечения конуса и цилиндра
На анимации ниже представлена последовательность построения линии пересечения конуса и цилиндра.
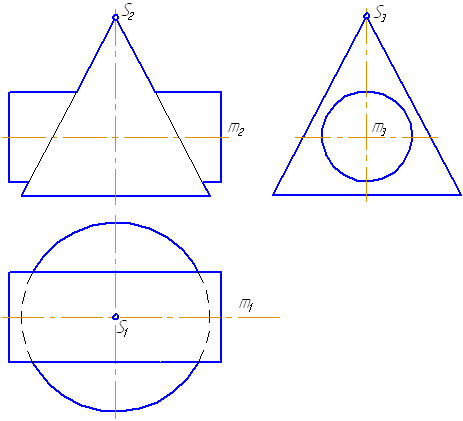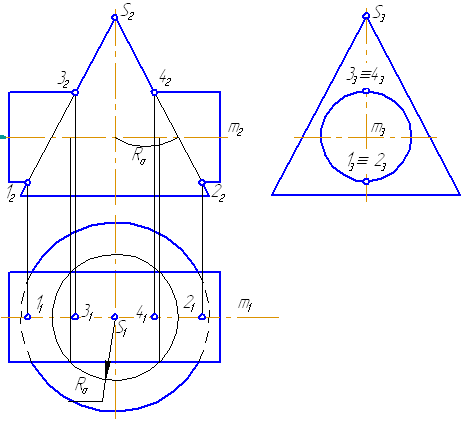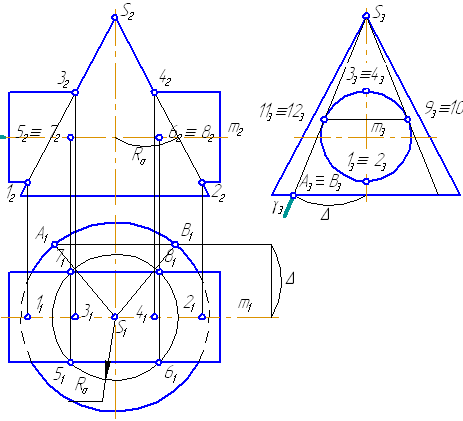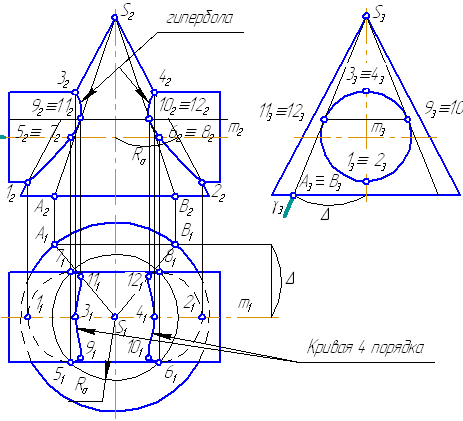
Рисунок 8.6 – Последовательность построения линии пересечения конуса и цилиндра
8.3. Задачи для самостоятельной работы
1-2. Построить линию пересечения поверхностей вращения (Рисунки 8.7, 8.8).
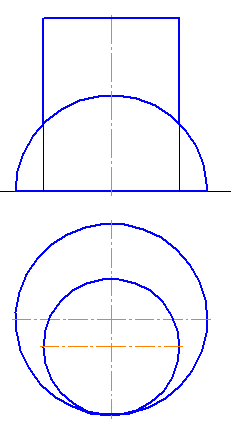
Рисунок 8.7
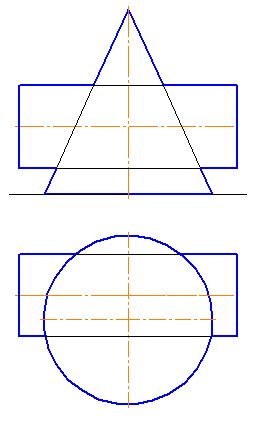
Рисунок 8.8




